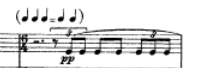I recently listened to this concert, the 66th of the current Proms season, featuring the Berlin Phil with Simon Rattle in the following program:
Wagner, Parsifal Overture
Strauss, 4 Last Songs
… and then, played without any break:
Schoenberg, 5 Orchestral Pieces
Webern, 6 Orchestral Pieces
Berg, 3 Orchestral Pieces
[I should mention before we go any further that the audio from this particular concert is available for only another 12 hours (i.e. you won’t be able to listen to it after Friday morning.)Â Sorry!]
I think this is really a hell of a program, and certainly an interesting choice for a Prom, given that those programs usually tend toward the populist side of things. But first off, if you end up listening to one of the Proms broadcasts on the BBC iPlayer, you’ll notice something a tad peculiar about the volume adjuster. This has got to be a joke, right?
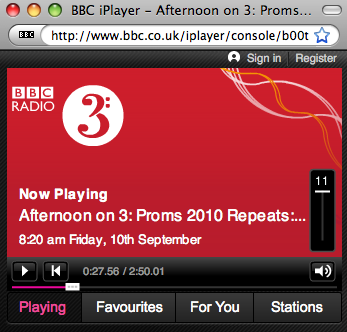
Or is their player really just louder?
My analytical juices started to flow when Sir Simon mentioned in his introductory remarks that the Parsifal Overture was in many ways the most rhythmically complicated piece on the program. This seemed like it might be kind of a stretch particularly because when you listen to it, it sounds like pure, unfettered melody with a subtle oscillation running underneath (like around 0:44).
But not being familiar with the Overture (or is it a Prelude?) myself, I decided to take a look at the score:

So now things start to get very interesting, because if you look at the flute part in the last bar, you see this:
which is one of these musical-mathematical conundra that conductors just love to stew over. See, what happens is that while the rest of the orchestra keeps playing in 4/4 – i.e. four quarter notes per measure – the flutes and two of the clarinets have to count 6 quarter notes to each measure. So, each of their quarter notes will end up being shorter/faster than the other players’ at a ratio of 6:4.
It would be easy enough if all they had to do was play 6 of their shorter, faster quarter notes against a conductor beating a four pattern of slightly slower quarter notes – musicians have to do this basic sort of trick all the time. But Wagner doesn’t make it that easy. Instead, he writes a rather complicated rhythmic figure (which, vexingly, will hardly even be heard in the orchestral texture.)
In this figure, the flutes and clarinets have to subdivide each of their six quarters into three triplet-eighth notes, so the total number of these notes in a bar is 6 x 3 = 18. This is all well and good, lest we forget that their visual and musical reference in lining up with the rest of the orchestra is 4 (quarter notes to the measure, that is). 18 ÷ 4 = 4.5. Since 4.5 isn’t a whole number, it’s not exactly useful.
Except that a particularly clever flautist bent on finding a practical solution to this problem (the problem being how to know how fast to play her triplet-eighth notes in a bar of six and line that up with the conductor’s four pattern) might notice something: despite the fact that 4.5 seems to bear little logical relevance to the problem at hand, if we take a closer look at the particular rhythm that she’s playing:
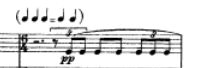 we notice that the second beat in this pattern consists of 2 eighth notes. So, one solution is to approximate the triplets and make sure that the second eighth lands on the conductor’s fourth beat. 1 eighth note = 1.5 of the triplets; therefore 3 triplets + 1 eighth equals 4.5 triplets.
we notice that the second beat in this pattern consists of 2 eighth notes. So, one solution is to approximate the triplets and make sure that the second eighth lands on the conductor’s fourth beat. 1 eighth note = 1.5 of the triplets; therefore 3 triplets + 1 eighth equals 4.5 triplets.
And that’s likely what everyone who actually plays this does, but the University of Chicagoan in me just hast to know the exact, theoretical answer, as practically untenable a solution as it may present. The next step is to multiply the 18 triplet-eighth notes by 2 – basically, we’re looking for a least common multiple between 18 and 4, i.e. 36.
So then, the really anal-retentive flautist, who probably has no job and definitely has like zero friends, if she were hired to play the Parsifal Overture (Prelude?) would sit at home and practice counting 36 notes per bar (that’s 9 notes per beat, btw), and regroup those 36-lets into twos so that she would wind up with 18 groups of 2 and divide those 18 groups by 3 so that she could feel 6 beats per bar and know that she had done a really thorough job. She might employ a chart that looked something like this:
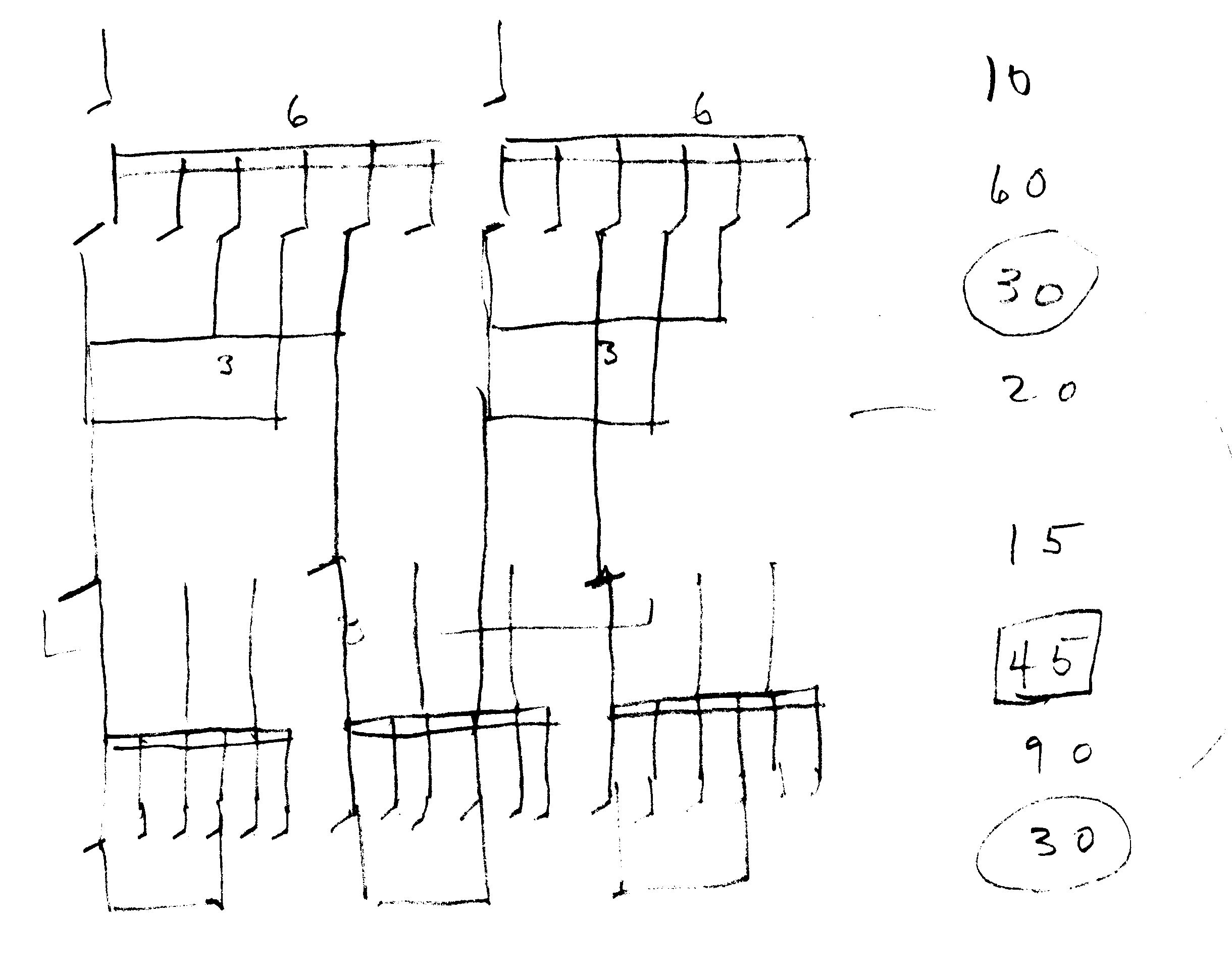
and still not be quite satisfied with the outcome. Now, if she really got to thinking smart, said flautist might decide to trip the conductor before he went on stage and step in for him, since beating a simple four pattern and letting everyone else worry about this crap is a way better idea. But she wouldn’t be able to escape her obsession – her obsession with rhythm. And now it would just get even worse, because did you see what was going on with those violas?? They play 8 notes to the beat, multiplied by 4 beats to the bar, so 24 notes in total per measure. Now our valiant flautist/conductor must find the least common multiple of 24 and 36 (it’s 72) if she wanted to figure out how the flute and viola parts really lined up.
I wonder if any conductor or musicologist or whoever has ever actually taken the time to figure out how these two parts line up by dividing the bar into 72 parts. I can only think of one conductor who I would even remotely suspicion of doing such a thing [who shall remain nameless.]
NEXT TIME: I rate Schoenberg, Webern and Berg. [Which I actually meant to do this time, but it seemed like things were getting a little intense already.] Somebody had to do it.